안녕하세요. Harry입니다.
본 포스팅의 목적은, 코딩테스트를 준비함에 있어 스스로 공부한 지식을 정리하고자 합니다.
앞서 정리한 DFS 알고리즘 기초 학습에 이어 코딩테스트에선 어떤 유형으로 등장하는지 정리한 내용을 올리고자 합니다.
이전 학습내용
[Algorithm] DFS 알고리즘(깊이 우선 탐색)&BFS 알고리즘(너비 우선 탐색)이란?
안녕하세요. Harry입니다. 본 포스팅의 목적은, 코딩테스트를 준비함에 있어 스스로 공부한 지식을 정리하고자 합니다. - 무슨 개념인지? - 개념이 나오게 된 배경은? - 그 개념은 왜 쓰는지? - 장점
hyem5019.tistory.com
1. DFS 알고리즘이란?
그래프 탐색 시 시작 노드부터 다음 분기로 넘어가기 전 해당 분기를 모두 탐색하고 넘어가는 탐색법이다.
결국 모든 노드를 방문하긴 할껀데, 어떤 순서로 방문할 것인가? 라는 물음에 "어디로 갈지 갈 길을 정한 후 해당 루트에서 갈 수 있는데까지 가보고, 더이상 갈 길이 없으면 다시 돌아와서 다른 길 가볼게요" 라고 답하는 알고리즘이다.
여기서 중요한 건 '그래프 탐색' 이라고 생각했는데, 그 이유는 아래 유형 분석 시, 그래프가 어떤 그래프냐에 따라 접근법이 조금씩 달라지기 때문이다.
2. DFS 알고리즘으로 풀 수 있는 유형의 종류
1) 2차원 좌표 그래프(선형구조)
선형 구조란, 자료를 구성하는 원소들을 하나씩 정렬한 것을 의미한다. 보통의 그래프는 비선형구조를 띄지만, 지도 등으로 표현되는 2차원 좌표 그래프는 선형구조라고 이해했다.
이런 좌표 그래프의 경우, 특정 요소간 연결과 배열이 일정하기 때문에 2차원 리스트를 생성하여 표현해주면 간편하다.
ex) graph = [[1,2,3],[4,5,6],[7,8,9]] 이라는 리스트는 좌표로 볼 때 아래와 같이 표현가능하다.
(통상 graph[x][y]로 표현하기 때문에, 고등학교때 배운, 흔히 우리가 쓰던 2차원 좌표 그래프와는 각도가 조금 다르다.)
graph[0][2] == 3
graph[1][1] == 5
graph[2][1] == 8
graph[2][2] == graph[-1][-1] == 9
사실 123/456/789 를 세로로 세우면 우리가 흔히 아는 x,y 좌표로 사용해도 되지만, 다들 그렇게는 안쓰는듯..?

이처럼 2차원 좌표를 활용해야하는 문제가 나온다면, 아래와 같은 조건을 생각해주는 것이 필요하다.
범위확인 -> 범위 내 돌아다닐 수 있는 길 확인 -> 돌아다닐 수 있는 방향 확인
(Base) def DFS(x,y):
(1) 주어진 좌표의 범위 확인(NxM 그래프)
- 주어진 범위를 벗어나면 return False
- 문제에서 주어진, 탐색할 수 없는 좌표(벽, 바다, 괴물이 사는 곳 등등)에 들어가면 return False
(2) 탐색하고자 하는 조건 확인(값이 0 인 곳만 탐색할 수 있다 등등)
- if graph[x][y] == 0:
graph[x][y] = 1 (방문 처리)
(3) 탐색할 수 있는 방향 확인(상하좌우, 또는 대각선으로 갈 수 있는지 등)
- 재귀함수를 통해 이동가능한 방향에서 다시 한 번 탐색 진행
ex) 상하좌우 1칸씩 이동 가능할 시
dfs(x+1,y)
dfs(x-1,y)
dfs(x,y+1)
dfs(x,y-1)
재귀함수를 호출해도 주어진 좌표 범위(1번 조건)에서 벗어난다면 자연스럽게 False 처리 됨.
def dfs(x,y):
#주어진 범위 확인
if x < 0 or x >= n or y < 0 or y >= m:
return
#탐색 조건 확인
if graph[x][y] == '-':
graph[x][y] = 1
#이동 조건 확인
dfs(x,y+1)
dfs(x,y-1)
return True
return False재귀함수 사용 시 재귀 깊이 제한을 늘려주기 위해 아래와 같은 코드작성이 필요하다.
import sys
sys.setrecursionlimit(10 ** 6)
2) 간선 그래프(비선형 구조)
간선 그래프 중에서도, 트리 등 상호 간 연결관계가 일관되지 않은 비선형 구조의 그래프를 의미한다.
이런 그래프의 경우 2차원 좌표 그래프로 표현하기에는 무리가 있으며, 2차원 리스트 내 인덱스 번호 = 노드 번호로 활용하곤한다.
ex) 아래와 같은 그래프의 경우
#연결된 노드의 정보
1 2
2 3
1 5
5 2
5 6
4 7graph = [list(map(int,input().split())) for i in range(문제에서 제시한 연결선의 정보)]
#인덱스 번호 그대로 노드 번호와 매칭하기 위해 range(n+1)을 활용한다.
map = [[] for i in range(n+1)]
for i in graph:
map[i[0]].append(i[1])
map[i[1]].append(i[0])map 이라는 2차원 리스트에 각각 연결된 노드 번호들을 넣어주는데, 1-2번 노드가 연결되어 있을 경우, map 리스트 1번 인덱스에 해당하는 리스트에 2 넣기 & map 리스트 2번 인덱스에 해당하는 리스트에 1 넣기 로 쌍방향으로 append해준다.
즉, map 리스트에서 각 인덱스에 해당하는 번호는 노드의 번호이고, 그 노드에 연결된 다른 노드번호가 2차원 리스트에 포함되는 것이다.
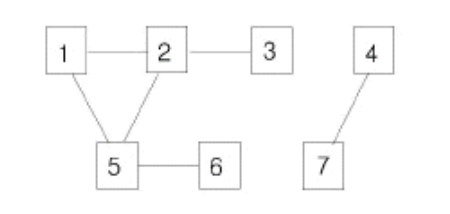
여기까지 한다면 print(map)을 했을 때 아래와 같이 나올 것이다.
[[], [2, 5], [1, 3, 5], [2], [7], [1, 2, 6], [5], [4]]이후에는 문제에 따라 map 리스트를 활용하는 방식이 다르지만, 통상적으로 map과 같은 크기의 빈 리스트 하나를 더 생성한 후
ex. visit = [ [False] * (n+1)]
아래 dfs 함수 를 통해 방문처리를 해주는 것으로 DFS 알고리즘을 구현할 수 있다.
def dfs(v):
visit[v] = True
for i in map[v]:
# visit[i]가 False라는 뜻
if not visit[i]:
dfs(i)
감사합니다.
'Coding Test > DFS,BFS' 카테고리의 다른 글
| [[Algorithm] ] BFS 알고리즘 기본 함수 작성 방법 (파이썬) (0) | 2023.02.14 |
|---|---|
| [DFS 알고리즘] 1388번 바닥장식 풀이(파이썬) (0) | 2023.02.01 |
| [Algorithm] DFS 알고리즘(깊이 우선 탐색)&BFS 알고리즘(너비 우선 탐색)이란? (2) | 2022.12.30 |
![[Algorithm] DFS 알고리즘(깊이 우선 탐색) 코딩테스트 문제 유형 분석(파이썬)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FwntTn%2FbtrYeZvFXYI%2FHweM7K4rHwhflk9k0l1wf1%2Fimg.png)